ریاضیات، انعکاس دنیای واقعی در ذهن ما
امیدوارم این مطالب برای شما مفید باشد و از ریاضیات لذت ببرید.

حساب دیفرانسیل و انتگرال و هندسه تحلیلی ریچارد سیلور من
اثبات تصویری اتحاد ها
کتاب حساب دیفرانسیل و انتگرال و هندسه تحلیلی توماس
دریافت
حجم: 3.25 مگابایت
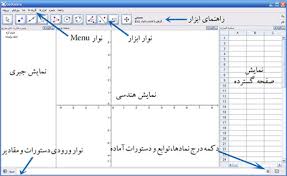
نرم افزار جئوجبرا
نرم افزار جپو جبرا توسط مارکوس هوهن وارتر در دانشگاه سالزبورگ اتریش و تیم همراه وی طراحی و اجرا شده است و به صورت رایگان در دسترس است. این نرم افزار یکی از مجموعه نرم افزارهای هندسة پویا محسوب می شود که مفاهیم هندسه، جبر و حساب دیفرانسیل و انتگرال را در محیط پویا با هم تلفیق کرده است. و هدف اصلی این نرم افزار نمایش چندگانه و بصری مفاهیم ریاضی می باشد. علاوه بر اینکه استفاده از نرم افزار جئوجبرا به دانش آموزان و معلمان در خانه و کلاس درس توصیه می شود. این نرم افزار ابزاری است که در سراسر مرزها در دسترس است. و به دسترسی برابر به منابع تکنولوژیکی و مردمی نمودن یادگیری و تدریس ریاضیات کمک می کند.
مقدمات جبر بازی با نخ
عدد پی
تاریخ عددپی، به محاسبه محیط و مساحت سطح دایره مربوط می شود. مصری های زمان دور از ما،از عدد پی برای حل مسئله هایی که در زندگی به کار می رفت ،استفاده می کردند. از متون قدیمی هم استنباط می شود که مردم سرزمین باستان بابل هم عدد پی را برابر 3 می گرفتند .این مقدار عدد پی، با توجه به اقتصاد آن روزگار، برای مصری ها و بابلی ها کافی بود و به دقت پیش از آن نیاز نداشتند. با پیشرفت نیروی تولید،دقت بیشتری برای عدد پی لازم بود و از جمله مصری ها مساحت دایره ای را که قطر آن برابر D باشد محاسبه می کردند که عدد پی به دست می آید.
این مقدار عدد پی، را در سده سوم پیش از میلاد ، ارشمیدوس یافت . بنا بر محاسبه او(عدد ارشمیدوس)، نابر محاسبه ارشمیدوس ،مقدار دقیق تر عددپی را به حساب آورد.
آپولونیوس(سده سوم پیش از میلاد)و بتلمیوس(سده دوم پیش از میلاد) ریاضیدانان یونان باستان،مقدار دقیق تری را برای پی یافتند.
موفقیت های بالاتر در زمینه محاسبه رقم های بیشتری برای عدد پی را دانشمندان ایرانی یافتند. انگیزه آن ها در این راه، تشکیل جدول های اخترشناسی و مثلثاتی بود. در سده نهم میلادی،خ وارزمی برای عددپی،مقدارهای تقریبی در نظر گرفت.
سپس بعدها در سده پانزدهم میلادی،جمشید کاشانی در رساله ای که درباره دایره نوشت(رساله المحیطیه)،عددپی را با 16 رقم درست پس از ممیز یافت.
براهما گوپتا،ریاضیدان هندی سده هفتم میلادی، پی را انتخاب کرد.
ویت ،ریاضیدان فرانسوی سده شانزدهم،عدد پی را با کمک چند ضلعی های منتظم با251658240 ضلع ،تا 10 رقم دهدهی از روی چند ضلعی های منتظم محاطی و محیطی که 251658240 ضلع داشتند،به دست آورد. سپس (رودلف) اهل (کلن) در آغاز،عددپی را تا 20 رقم دهدهی و بعد تا 35 رقم دهدهی پیدا کرد،این عدد را (عدد رودلف)می گویند.
ریاضیدانان سده 18و 19، عددپی را با رقم های بسیاری بیشتری محاسبه کردند که در عمل به کار نمی آید و برای این بود که ببینند آیا قانونی بر رقم های آن جاری است!
لابرت ریاضیدان آلمانی در سال 1761،گنگ بودن عدد پی را ثابت کرد. آدرین-ماری لژاندر ثابت کرد که مجذور پی هم عددی گنگ است. سرانجام لیندمان ریاضیدان آلمانی ،غیر جبری بودن عدد پی را ثابت کرد، یعنی نمی تواند ریشه یک معادله با ضریب های گویا باشد.
از کتاب اعداد در ریاضیات نوشته شقایق خوشبخت
موسیقی عدد پی
یک مایل عدد پی
عدد پی در آسمان
ریاضیات در طبیعت
اعداد در طبیعت